本文共 1110 字,大约阅读时间需要 3 分钟。
title: 斯坦福-随机图模型-week2.0
tags: note notebook: 6- 英文课程-9-Probabilistic Graphical Models 1: Representation ---斯坦福-随机图模型-week2.0
模板模型(Template Models)
在实际的模型的建立的过程中,会出现很多的重复的情况。比如在如下的模型中:
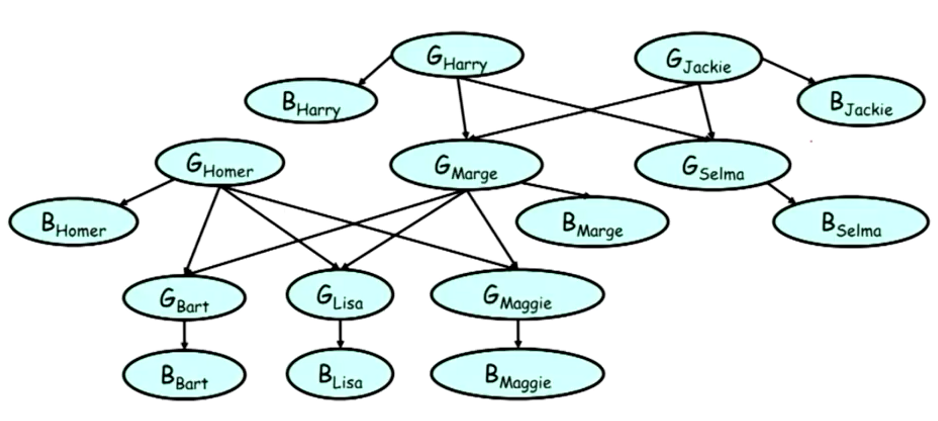
有很多的重复的结构,比如每一个的基因型都和表现形直接相关。而且每一个基因型都和两个前代的基因型十分的相关。
或者在自然语言处理的模型中:
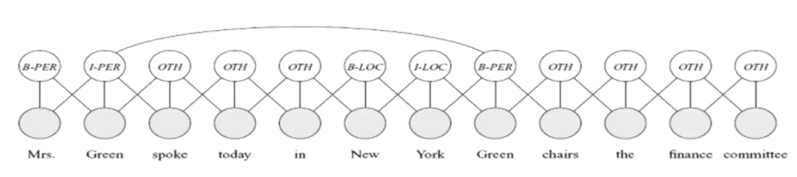
在序列模型中,每一个原包也都有很多的辨别是不是名词和其本身的结构也都有固定的概率联系,这些问题都可以用模板模型讨论。
在图像处理中也是这样,我们并不想给每一个超像素建立一个独立的模型,因此我们应该通过某些方式将这些权值共享起来。
通过轨迹的分布
- 选择一个时间间隔
-
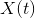 事在t时间内的变量x的值
事在t时间内的变量x的值 -
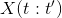 是一段时间的值的向量
是一段时间的值的向量
马尔科夫推断
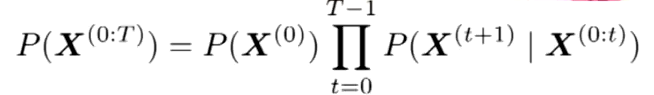
马尔科夫推断是一个推断链条,他的意思是,从x0-xn发生的概率是xo发生的概率,乘以x0发生的情况下x1发生的概率,乘以x1以前发生的情况下x2发生的概率,以此类推。
不过我们在这里有一条假设,就是t+1时刻于t-1时刻对于t时刻是条件独立的。
在这个假设下我们可以将我们前面的公式进行简化。
简化成了这个样子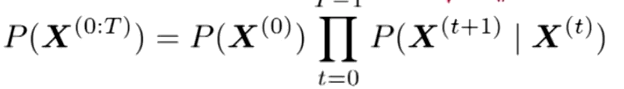
但是在现实的情况下,这样的假设是不能成立的,比如我们要讨论机器人的位置问题,机器人之前的状态和将来的状态是相互独立的吗?
如何解决这个问题呢?
有一个就是我们可以给他的行动增加独立性,建立一个半马尔科夫模型。不过我们先不讨论这个
time invariance 时间不变性
如果我们可以通过一个模型描述钱一个时间对后一个时间的影响。我们就可以建立一个模型对整个的状态进行描述。
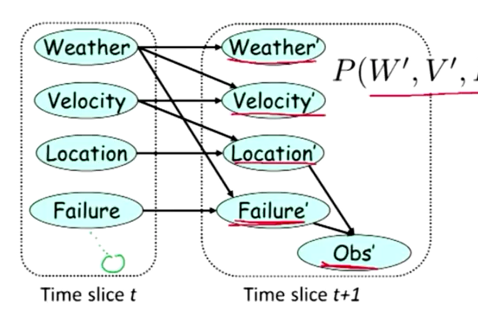
就像这样,我们建立这样的一个模型来描述前一个时间与下一个时间的各个变量的关系。
通过链式法则,我们可以连续的将时间向后推进,就像这样:
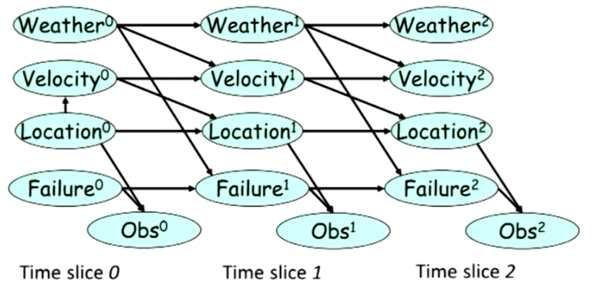
隐马尔科夫模型
在这样一个模型中:
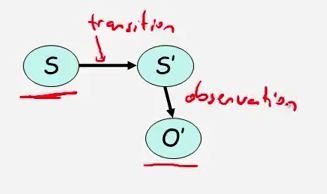
s通过转换变成s‘
然后通过观测变成o’那我们的模型就有两个部份,一个是转换模型,一个是观测模型。同样的我们可以将这些模型进行复用。变成这个样子
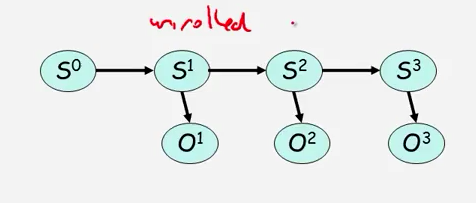
这用模型的用途是什么呢:
- 机器日的位置
- 速度探测
- 生物序列分析
- 文本分析
机器人的位置
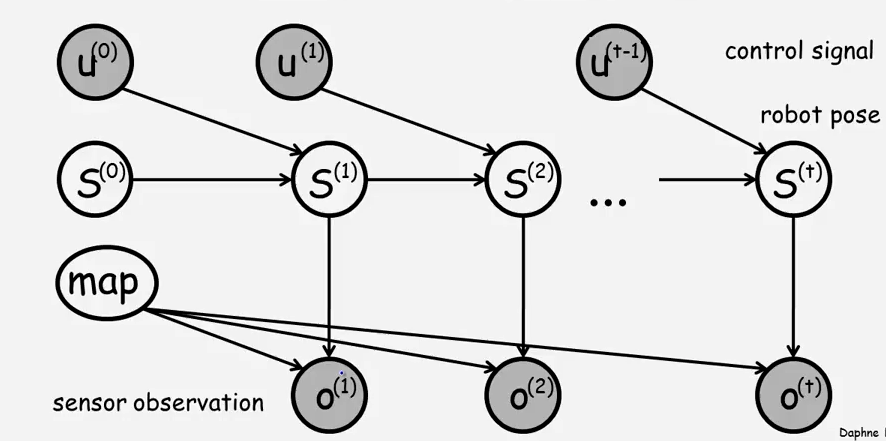
机器人的位置模型可以这样描述,我们看到s是现在的位置,或者状态,它可以用很多的量来描述,比如说现在的速度,位置,加速度等等,
u是控制信号,用来改变机器人的上述变量。从而藐视下一时间段的机器人的位置。总结
- HMM模型可以看成是DBN模型的一个特里
- 他将随机变量进行了简化
- 应用十分广泛
转载地址:http://zlazx.baihongyu.com/